|
|
||||||||
|
Keynote Part II
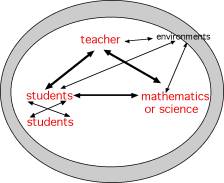
Using Content Knowledge in Teaching: What Do Teachers Have to Do, and Therefore Have to Learn?Part IIDeveloping a Practice-Based Approach to Learning Content for Teaching If we assume that what matters here is teachers' ability to solve the actual problems of their work and to use mathematics and science in the course of that work, then it seems logical we would want approaches to teacher education and professional development that help teachers learn to do that and not simply improve their own knowledge as human beings. It would be important to find ways to prepare teachers professionally for the mathematical and scientific problem solving of their work. In the field of mathematics, for example, this is not so different from the way we think about the education of other mathematics professionals, such as engineers, biologists, economists, and nurses, all of whom use mathematics in their work. In professional education for these fields, we specifically design coursework that aims to prepare people for the mathematical applications required by their work. Teaching can also be seen as a field involving significant applications of mathematics. What it would look like to develop professional education that gave teachers of mathematics the mathematical skills to do the specialized problem solving endemic to mathematics teaching? What would professional education look like that developed science teachers' scientific capacities for the problems of science teaching? Background: A Portrayal of Teaching and Professional Education for Teachers The diagram below is a portrayal of "teaching" and is used here to orient you to the way that we'll talk about professional development in this discussion:
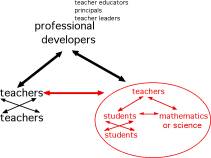
One thing to notice in this depiction is that teaching is shaped by the interactions among these elements - the teacher, students, subject matter, and environment5. If a teacher poses a task to a group of students, how the students understand what the teacher says shapes what the work actually becomes. A task doesn't play out the same way in every classroom because it depends on what students bring to it, what they ask their teacher, what their teacher says back. How the teacher understands the mathematics or science, shapes how she might hear her students; it influences what she might know to do in launching the task or managing how it plays out; and it makes a difference in the way she makes judgments - even about highly scripted curriculum materials. The teacher's comprehension of the content shapes what the students have access to. Teaching, as it is portrayed here, is highly dynamic. The mathematics and science doesn't live apart from the work of teaching but is deeply inside it in all the interactions between teachers and their curriculum materials, teachers and their students, and even teachers and their interpretations of factors in the environment. Here's the same diagram again, used now to model "instruction" in the context of professional education for teachers.
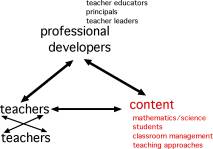
In this diagram, teachers are now the learners, professional developers are the teachers, and instead of thinking, "Let's teach them mathematical content," what we're actually trying to think about is how we would help teachers acquire the disciplinary knowledge and skills of their practice. In this case, practice becomes the medium for professional development. "Practice" might mean a teachers' own practice, or it might mean a written case of a classroom episode, examples of student work, or a videotape of a lesson. It might mean the close instructional design and analysis involved in collaborative lesson study work. What makes these similar is that they all use the work of teaching itself, in some way, as the ground for developing teachers' capacity.6 This diagram was meant to illustrate the notion that when we organize professional development more around practice, it's closer to the work teachers do and therefore, we conjecture, more likely to be usable. I'd like to contrast this perspective on professional development with one that is much more common, one we might call learning by acquiring new knowledge. This view focuses on equipping teachers with new knowledge or information -- for example, about content, about instructional approaches, about students' learning, conceptions, or experience. This way of thinking about professional development assumes that what teachers need is knowledge, and is designed in ways to help them acquire it. It is assumed that their practice will be affected by this new knowledge.
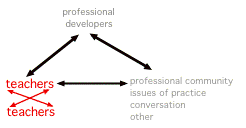
Another popular way of thinking about professional development is to understand teachers' opportunities to work with colleagues as the central resource for the improvement of their practice. This perspective leads to efforts to make time available for teachers to collaborate and assumes that they will be able to provide guidance and support for one another (i.e., play the role of "professional developer" for themselves) and that they will select and be able to learn things that will help them with their practice.
What is interesting is that neither of these perspective on teachers' learning is "wrong." Of course knowledge can be a crucial resource. And of course working with colleagues can be a deeply important source of learning. But a focus on teachers' learning in and from practice does not preclude a concern for the development of new knowledge nor work with colleagues. Quite the contrary: it embraces both. However, what this perspective, represented in the first diagram makes central is use, broadly defined. It takes as crucial the connections to teachers' work. From this perspective, content knowledge emerges in its interaction with interpreting students' ideas, working with curriculum materials, deciding what to do with unexpected moments in a lesson. Teachers' opportunities to learn content are connected in some way to the use of that content in teaching. 5 This diagram comes from work I have done over the past several years with David Cohen on the nature of instruction and instructional innovation. We refer to this as the “instructional triangle,” and use it to emphasize the dynamic nature of instruction, shaped by the interactions among students, teachers, and the content, in particular environments. See, for example, Cohen, D. K., & Ball, D. L. (2001). Making change: Instruction and its improvement. Phi Delta Kappan, 83 (1), 73-77. It is also found in chapter 9 of Adding It Up: How Children Learn Mathematics, the National Research Council report, published in 2001, edited by Jeremy Kilpatrick, Jane Swafford, and Bradford Findell. 6 This idea of “learning in and from practice” is elaborated in Ball, D. L. & Cohen, D. K. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In G. Sykes and L. Darling-Hammond (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3-32). San Francisco: Jossey Bass. |
||||||||||||||||||||||||||
| © TERC 2003, all rights reserved | Home • Keynote • Poster Hall • Panels • Discussants Reflect • Resources • Lounge • Info Center |