|
Table of Contents: |
||||||||
Developing a Practice-Based Approach to Learning Content for Teaching
If we assume that what matters here is teachers' ability to solve the actual problems of their work and to use mathematics and science in the course of that work, then it seems logical we would want approaches to teacher education and professional development that help teachers learn to do that and not simply improve their own knowledge as human beings. It would be important to find ways to prepare teachers professionally for the mathematical and scientific problem solving of their work. In the field of mathematics, for example, this is not so different from the way we think about the education of other mathematics professionals, such as engineers, biologists, economists, and nurses, all of whom use mathematics in their work. In professional education for these fields, we specifically design coursework that aims to prepare people for the mathematical applications required by their work. Teaching can also be seen as a field involving significant applications of mathematics. What it would look like to develop professional education that gave teachers of mathematics the mathematical skills to do the specialized problem solving endemic to mathematics teaching? What would professional education look like that developed science teachers' scientific capacities for the problems of science teaching?
Background: A Portrayal of Teaching and Professional Education for Teachers
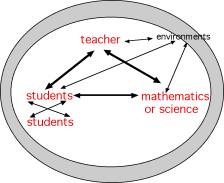
The diagram below is a portrayal of "teaching" and is used here to orient you to the way that we'll talk about professional development in this discussion:
| Knowing and using mathematics and science in teaching |
|
One thing to notice in this depiction is that teaching is shaped by the interactions among these elements - the teacher, students, subject matter, and environment5. If a teacher poses a task to a group of students, how the students understand what the teacher says shapes what the work actually becomes. A task doesn't play out the same way in every classroom because it depends on what students bring to it, what they ask their teacher, what their teacher says back. How the teacher understands the mathematics or science, shapes how she might hear her students; it influences what she might know to do in launching the task or managing how it plays out; and it makes a difference in the way she makes judgments - even about highly scripted curriculum materials. The teacher's comprehension of the content shapes what the students have access to. Teaching, as it is portrayed here, is highly dynamic. The mathematics and science doesn't live apart from the work of teaching but is deeply inside it in all the interactions between teachers and their curriculum materials, teachers and their students, and even teachers and their interpretations of factors in the environment.
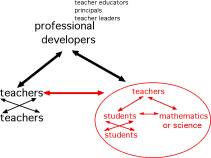
Here's the same diagram again, used now to model "instruction" in the context of professional education for teachers.
| Learning in and from practice |
|
In this diagram, teachers are now the learners, professional developers are the teachers, and instead of thinking, "Let's teach them mathematical content," what we're actually trying to think about is how we would help teachers acquire the disciplinary knowledge and skills of their practice. In this case, practice becomes the medium for professional development.
"Practice" might mean a teachers' own practice, or it might mean a written case of a classroom episode, examples of student work, or a videotape of a lesson. It might mean the close instructional design and analysis involved in collaborative lesson study work. What makes these similar is that they all use the work of teaching itself, in some way, as the ground for developing teachers' capacity.6
This diagram was meant to illustrate the notion that when we organize professional development more around practice, it's closer to the work teachers do and therefore, we conjecture, more likely to be usable.
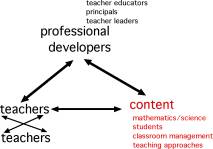
I'd like to contrast this perspective on professional development with one that is much more common, one we might call learning by acquiring new knowledge. This view focuses on equipping teachers with new knowledge or information -- for example, about content, about instructional approaches, about students' learning, conceptions, or experience. This way of thinking about professional development assumes that what teachers need is knowledge, and is designed in ways to help them acquire it. It is assumed that their practice will be affected by this new knowledge.
| Learning by acquiring new knowledge |
|
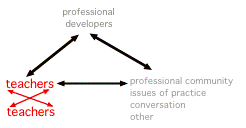
Another popular way of thinking about professional development is to understand teachers' opportunities to work with colleagues as the central resource for the improvement of their practice. This perspective leads to efforts to make time available for teachers to collaborate and assumes that they will be able to provide guidance and support for one another (i.e., play the role of "professional developer" for themselves) and that they will select and be able to learn things that will help them with their practice.
| Learning through collegial interaction |
|
What is interesting is that neither of these perspective on teachers' learning is "wrong." Of course knowledge can be a crucial resource. And of course working with colleagues can be a deeply important source of learning. But a focus on teachers' learning in and from practice does not preclude a concern for the development of new knowledge nor work with colleagues. Quite the contrary: it embraces both. However, what this perspective, represented in the first diagram makes central is use, broadly defined. It takes as crucial the connections to teachers' work. From this perspective, content knowledge emerges in its interaction with interpreting students' ideas, working with curriculum materials, deciding what to with unexpected moments in a lesson. Teachers' opportunities to learn content are connected in some way to the use of that content in teaching.
5 This diagram comes from work I have done over the past several years with David Cohen on the nature of instruction and instructional innovation. We refer to this as the 'instructional triangle', and use it to emphasize the dynamic nature of instruction, shaped by the interactions among students, teachers, and the content, in particular environments. See, for example, Cohen, D. K., & Ball, D. L. (2001). Making change: Instruction and its improvement. Kappan, 83 (1), 73-77. It is also found in chapter 9 of Adding It Up: How Children Learn Mathematics, the National Research Council report, published in 2001, edited by Jeremy Kilpatrick, Jane Swafford, and Bradford Findell.
6 This idea of –learning in and from practice” is elaborated in Ball, D. L. & Cohen, D. K. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In G. Sykes and L. Darling-Hammond (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3-32). San Francisco: Jossey Bass.
An Example of Using Video to Learn Mathematics for Teaching
What I'm going to try to do next is take one example of what it might look like to organize professional development around practice. In this case, I'm going to use a video clip. However, I don't want to give the impression that I am arguing that learning in and from practice requires the use of video cases. I'm not saying that at all. I'm only proposing video as one way of capturing practice and making it available for use in professional development. As I mentioned above, another way to ground professional education in practice is to read and discuss cases; another way to do it is to engage in lesson study - and an increasing number of lesson study groups are emerging in this country; another way is to work with study groups of teachers in schools. The overarching idea here is to organize professional development much closer to the work of teaching. My use of a video clip here is one example of how one might do that.
The challenge is this: By now, many of us are familiar with the idea of using video in professional teacher education, however, we don't always think of using video to create opportunities for learning content. Rather, it is more common to use video to discuss children's thinking, or to examine the teacher's moves, or to talk about teaching practice. What we will do here is explore what it might look like to design opportunities for teachers to learn mathematics from a piece of video.
This is the list I showed you earlier with examples of mathematical problems teachers face in their work:
| What Mathematical Problems Arise in Teaching? |
Examples
|
The ones we focused on earlier are shown in red: Analyzing errors, choosing and using definitions, and appraising claims. Now we're going to switch to and work on the four highlighted here (in green) as we examine a kind of activity that might be used in professional education.
The example we are going to explore involves using records of practice - in this case, a video.
|
Example:
Using Records of Practice to Study Mathematics for Teaching |
I am going begin by framing the video clip for you. Then, after watching the video, we will look at some different examples of work that could be asked of teachers in a teacher education course or in a professional development setting that focus on mathematics learning. You might try to attend to the mathematical issues that arise for you as you watch the clip -the tasks I'll show you will be related to mathematical issues embedded in the video.
This video comes from early May in a third grade class. It's ten days into the fractions unit and this is a curriculum where fractions are introduced for the first time in third grade, so this is relatively early in students' work on fractions. It's a classroom that's diverse, with many English language learners. The last page of the transcript gives you a bit of a portrait of who was in class on this day, their relative levels of English acquisition, their race, and so on. This will give a sense of the diversity of the classroom. It's also useful to say that this is a classroom in which the following norms were central components of the teaching and learning efforts across the entire school year: taking mathematics seriously; attending to other students' ideas with care; and working together on mathematics.7
|
Video Clip from 3rd Grade Lesson on Fractions |
|
In the previous class session, students were working on this problem: Here's a box of twenty-four crayons; how many crayons would be in half a box, a quarter of the box, a third of the box, two-thirds of the box, three quarters of a box, or one and half boxes?
|
||||||||||
It's important for you to know, as you watch this clip, that the students had been able to correctly answer, discuss, and justify their answers to one half, one fourth, one third, and three fourths of a box. The class ended before the students had a chance to discuss two thirds and one and a half boxes but they seemed to have no real difficulties with the problems they did discuss - including the last problem, three fourths of twenty-four.
The problem they were asked to solve on the day we're going to watch is, "How many in three quarters of a dozen?" - one dozen, not twenty-four, crayons. I'd like you to attend to the mathematical issues you notice as you watch the video.
| Designing Opportunities to Learn Mathematics From the Study of a Video Clip |
|
What mathematical issues do you notice in this video clip? |
After watching the video, I'll frame a set of tasks that might be used with this clip to work on learning mathematics for teaching. We'll use this to consider one way in which teachers' opportunities to learn content can be structured in and around practice, and to spur the discussion of other ways to design for such learning opportunities.
[Please watch the video clip now.]
What are some of the mathematical issues you see in the video?
7 This videotape is taken from a collection of records that spans the entire school year for this third grade class. With support from the National Science Foundation, lessons were videotaped daily from September through June, students' written work and drawings copied and saved, and teachers' plans and notes, the mathematics problems on which students worked, and many other elements of the class were carefully documented in order to study teaching and learning, and to explore ways in which such records might be used in teacher education and professional development.
Examples of Tasks for Learning Mathematics for Teaching Based on the Video
This video could obviously be used to launch a variety of pedagogical discussions: Did the teacher make good judgments? Why was time being used the way it was? We're more accustomed to that sort of use of video. What we're going to try to do right now is something that's a little less typical: We're going to use this video to focus specifically on mathematics. The argument for this focus is that one way to help teachers be prepared to use mathematics in their teaching is to engage them in solving problems of mathematics in the context of classroom teaching. This is not unlike the argument that children's mathematics learning can be enhanced by providing them with significant opportunities to apply and use mathematics in the context of specific, credible problems.
I'm going to propose six different tasks that could be used with teachers. Please work through as many as you would like. You might try them working together with a colleague at your location. Additionally, "discussion threads" have been set up for each task. I encourage you to spend some time working on the problem posed in the task with other conference participants who share your interest in exploring a particular task. Pay attention to the kind of mathematical work the problems entail, and the mathematical reasoning and ideas you are using as you try to address the questions. We'll conclude by talking about the sort of professional education this might provide if we did more problems of this type in the mathematical work we give teachers.
So here are the first three tasks -
What are some of your observations about these tasks?
What opportunities for learning mathematics do you notice?
What I'd like to do before wrapping up is to take these six tasks and to say a few things about the sort of mathematical problem solving that they require and then put a couple of caveats into what we've done together so far.
Let's just look through these six tasks. The following chart summarizes an initial analysis of the mathematical learning opportunities that may be embedded in work on each of these tasks:
| Solving Problems in Learning Mathematics for Teaching | |
|
#1: Sean uses a graham cracker to explain the meaning of three fourths to Riba. He also considered a dollar. Analyze and compare each as a mathematical representation of the meaning of 3/4. | Comparing representations, investigating correspondences among representations |
|
#2: Why do some of the students want to vote? Why do some object to voting? What are the mathematical issues here? | Interpreting student thinking; concepts of mathematical reasoning |
|
#3: The teacher uses 1/2 of 6 to help Riba reason about the meaning of three fourths. Analyze the mathematical considerations in this move. Is there another move that would be preferable mathematically? | Posing a question to scaffold student thinking, choosing specific numerical examples |
|
#4: Yesterday the class successfully reasoned about fractions of 24. What mathematical reasons are there to work on three quarters of 12 in today's lesson? What would be another question, and what does it offer mathematically? | Posing task to assess and develop students' thinking, choosing specific numerical examples |
| #5: What problem or question would be useful to pose to the class next? | Designing sequential tasks, choosing specific numerical examples |
|
#6: What can you say about each of the following students' understanding of some mathematical issue discussed in this clip? (Keith, Sean, Sheena, Daniel, Mei, Riba) | Interpreting students' mathematical thinking and understanding; identifying and naming particular mathematics |
If you think about the list I was offering earlier about problems of teaching, the first task about the graham cracker and the dollar can involve teachers in learning to compare representations and investigating the correspondences among representations. It's interesting: They both (the graham cracker and dollar bill) produce rectangles but they're not completely identical as contexts for representing of one fourth or three fourths. It's useful to think in detail about what the salient differences might be. Often, when teachers haven't had that opportunity, they seize one representational context without actually having noticed the subtle differences that there can be between a graham cracker that doesn't, for example, have the association with "quarters" which are inside of the dollar. And yet, dollars aren't something one literally breaks. It's interesting to think through the consequences of these differences even though graphically they look similar. And one can do some useful work thinking more closely about the nature of representation.
The second one, about "voting," may seem to be largely a pedagogical question and it could be difficult to orchestrate a discussion of this problem and keep it from being just that, but there are important mathematical questions here that arise in interpreting students' comments. What are the children actually saying when they talk about "voting"? What are the issues around mathematical reasoning, justification, and proof that might lead the teacher to think carefully about what to do in this situation? Many of us would say, voting is not what you do to decide mathematics and would want to shut it down quickly but the students' comments, if one were to listen carefully, suggests there may be more to hear in what they are saying and proposing to do. It suggests a teacher might be required to do some careful analysis about the nature of collective mathematical work and what it means to reason as a group.
The third task focuses on the question the teacher posed about "one half of six." This is an example of posing a question to scaffold student thinking and choosing specific numerical examples. We give far too little time and attention to the significance of the numbers we pick in the problems and examples we develop. Teachers are frequently in the position of needing to quickly pull together an example, when in the middle of something, and there are big consequences for those choices. More practice in becoming sensitive to and skillful at picking numbers - whether it's on the fly or in advance of class - could be useful. These on-the-fly decisions need to be made by teachers no matter how scripted the curriculum, therefore noticing that this is an important and consequential piece of mathematical judgment, having practice in doing this work, and talking carefully about these decisions seems worthwhile. In addition, it's not obvious that "one half of six" was a good choice so, if it wasn't, what were its problems? What would be a better alternative?
The fourth task, concerning the nature of the question the students were working on, is another example of thinking about specific numerical examples. The class had just worked on fractions of twenty-four the previous day so what was involved in talking three fourths of twelve that might have been different? How did it compare? Might there have been another question that would follow better from the children's work on fractions of twenty-four? If so, what is it? What opportunities and possibilities does it afford? This requires a lot of careful thought about the relationship between three-fourths and twelve - in particular, the relationship of the three and the four to the twelve and the three fourths is worth examining. Again, this task would provide practice with specific numerical reasoning.
The question of what problem to do next (i.e. the fifth task) is still in that same family but a little different. It has to do with thinking about the sequencing of mathematical ideas. "So, what's the next problem?" is slightly different than, "What's the question to ask during class?" It again might involve teachers in some detailed thought about numbers and examples. However, this also provides the opportunity to consider what might be the next mathematical question that follows from three fourths of twelve. What's the next kind of problem?
And, finally, looking closely at students (the sixth task) is also a way to work on mathematics for teaching. When you ask a question like, "Can you describe something that Keith seems to understand?" it requires the development of more insight into the mathematics: What is there to describe about Keith? What sorts of mathematical things did he say? How would you identify these things and label them? Learning to talk about the mathematics of students' thinking is also mathematical work. If one doesn't have this mathematical component, one is left with saying very vague things like, "Keith seems to be doing well" or, "Keith seems to understand the basic concept." This is not particularly helpful - it is neither helpful for talking to other professionals about Keith nor for working directly with Keith. Learning to discern what mathematics there is to notice in what a child does is mathematical work.
This is meant as an illustration of designing tasks for teachers as learners of mathematics, in and close to practice. These are a few examples of tasks that could be designed for use with teachers if one's goal was to work on mathematics for teaching.
A caveat is important here: Just as giving tasks to children doesn't necessarily help them learn mathematics, simply giving tasks such as these to teachers won't necessarily help them learn mathematics for teaching either. Still remaining is the need to consider is how one might scaffold teachers' work on these problems so that their work will lead to productive mathematical learning. How would one have to steer a professional development session so that the question and the discussion stayed on the mathematics and actually moved toward greater mathematical skill and understanding? We didn't do that here. All we have done so far is to look at some examples of problems that could be offered. The work that lies ahead of us is to talk about how would we use these kinds of problems and toward what ends.
Conclusions
Let me wrap up now with four conclusions:
One point I hope I didn't overdo but did emphasize enough to make an impression is that the content knowledge needed for teaching is different from that which is needed for other mathematically or scientifically intensive professions -- like engineering or medicine. It is mathematically and scientifically intensive work, but it requires a different kind of mathematical and scientific knowledge than that required for other forms of work.
The second point I tried to emphasize is that content knowledge has to be usable for the work that teachers do. Simply increasing teachers' content requirements or the time spent on subject matter in professional development without its connection to use isn't likely to produce very helpful results.
The third point that we spent quite a lot of time on was a claim that mathematics teaching involves specialized mathematical problem solving that we have less experience at seeing, noticing and designing opportunities to support. I hope we can talk more about what the analogies and correspondences are -- as well as what may be some of the differences --as we consider the teaching of science.
And finally, learning content for teaching can be better grounded in practice by designing opportunities for teachers to solve the content-related problems that arise recurrently in their practice. This is what we did at the end - we looked at some examples of how one could design such problems. We still need to talk more about how one could use such problems to help teachers learn content for teaching.
| Conclusions |
|
1. Knowledge needed for teaching is different from what is needed for other occupations or professions where scientific or mathematical knowledge is used (e.g., physics, mathematics, carpentry, tailoring, business).
2. Knowledge needed for teaching must be usable for the content-based work that teachers do. 3. Mathematics teaching involves specialized mathematical problem solving. Science teaching also involves scientific sensibilities, skills, ideas, and orientations. 4. Learning content for teaching can be grounded in practice by designing opportunities for teachers to solve content-related problems that arise recurrently in teaching. |